1. Softmax 求导

softmax层输出为 🌊

$a_j^L = \frac{exp(z_j^L)}{\sum_k exp(z_k^L)}$

其中$z_j^L$表示第L层第j个神经元的输入，$a_j^L$表示第L层第j个神经元的输出，求$a_j^L$对$z_j^L$的导数
如果j=i,

$\begin{aligned} \frac{\partial a_j}{\partial z_i} &= \frac{\partial}{\partial z_i}(\frac{exp(z_j)}{\sum_k exp(z_k)})\\ &=\frac{exp(z_i) \sum_k exp(z_k) - exp(z_i)exp(z_j)}{(\sum_k exp(z_k))^2}\\ &= a_j - a_j^2\\ &= a_j(1-a_j) \end{aligned}$

如果$j\ne i$

$\begin{aligned} \frac{\partial a_j}{\partial z_i} &= \frac{\partial}{\partial z_i}(\frac{exp(z_j)}{\sum_k exp(z_k)})\\ &= \frac{-exp(z_j)exp(z_i)}{\sum_k exp(z_k)}\\ &= -a_ja_i \end{aligned}$

2. cross-entropy求导

loss function为$l = -\sum_k y_kloga_k$
$\quad$ 对softmax层的输入$z_j$求导，如下

$\begin{aligned} \frac{l}{z_j}&= \frac{\partial}{\partial z_j}(-\sum_k y_kloga_k)\\ &= -\sum_k y_k \frac{1}{a_k} \frac{\partial a_k}{\partial z_j}\\ &= -y_j . \frac{1}{a_j}.a_j.(1-a_j) - \sum_{k\ne j}y_k . \frac{1}{a_k} . \frac{\partial a_k}{\partial z_j} \\ &= -y_j + y_j a_j + \sum_{k\ne j}y_ka_j\\ &= -y_j+a_j\sum_k y_k = a_j - y_j \end{aligned}$

3. label smoothing

对于ground truth为one-hot的情况，使用模型去拟合这样的函数有两个问题，首先是无法保证模型的泛化能力，容易导致过拟合；其次全概率和零概率将鼓励所属类别和非所属类别之间的差距被尽可能的拉大，因为模型太过相信自己的预测。（overconfidence）这时模型认为判断正确的输出在反向传播时没有影响。
为解决这一问题，使得模型没那么肯定，提出了label smoothing。
原ground truth为$y(k|x) = \delta_{k,y}$，添加一个与样本分布无关的分布$u(k)$，得到

$y^{'}(k|x) = (1-\epsilon)\delta_{k,y} + \epsilon u(k)$

用$\hat{y}(k|x)$表示预测结果，则loss function为

$l(y^{'}, \hat{y}) = -\sum_{k=1}^{K} y^{'}(k)log\hat{y}(k) = (1-\epsilon)l(y, \hat{y}) + \epsilon l(u, \hat{y})$

label smoothing出自论文《Rethinking the Inception Architechture for Computer Vision》，label smoothing使交叉熵增大，降低overconfidence带来的影响。

​

Seq-to-Seq中Coverage详解

最早出现在NMT中，在ASR应用中引入语言模型时会导致转写结果不完整（如homophone同音异形词情况，容易导致在decoding过程beam-search中剪枝过程忽略正确答案），引入coverage可以有效缓解
出自ACL2017一篇文章Get To The Point: Summarization with Pointer-Generator Networks
提出pointer-generator机制，这种pointer softmax相当于加入惩罚项，弥补上述提出的转写结果不完整的不足。
以下是传统Seq2Seq机制框架图

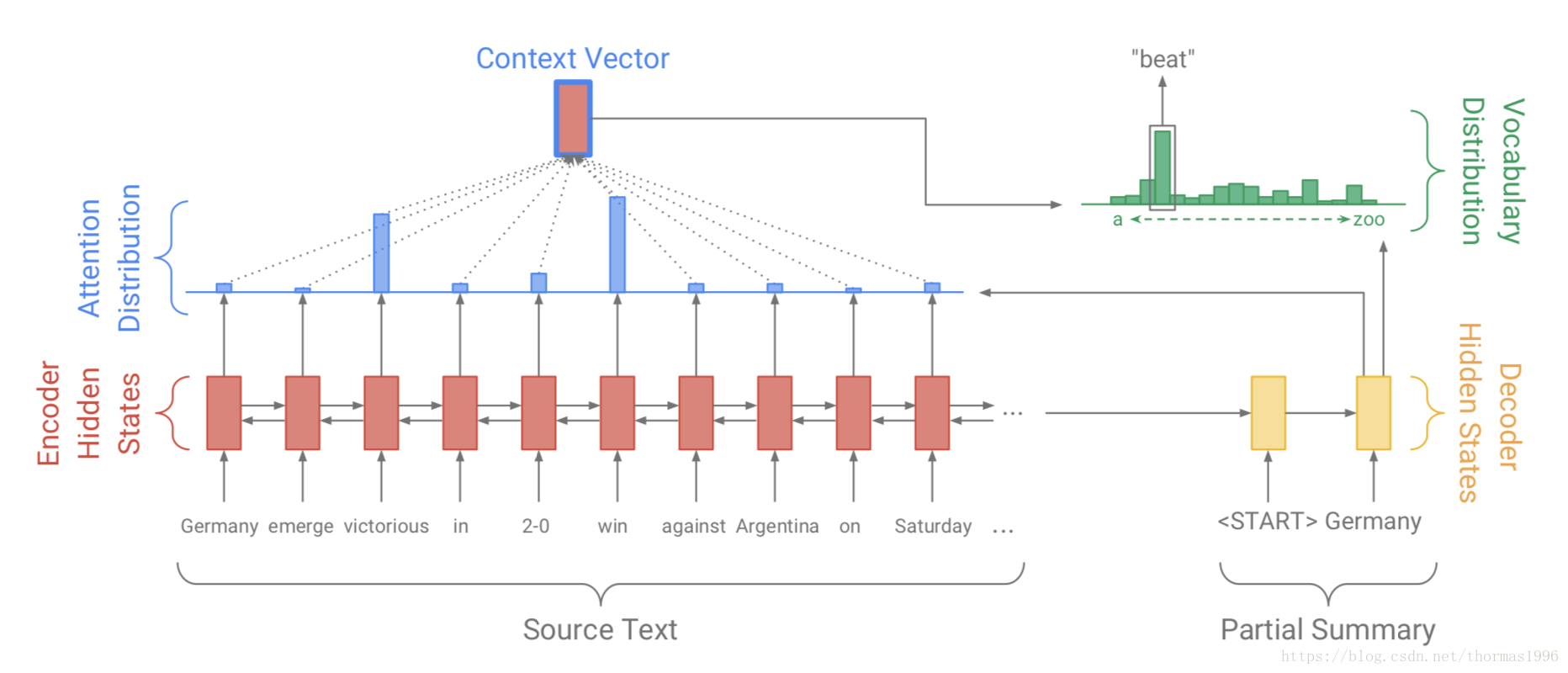
加入coverage后的原理图如下

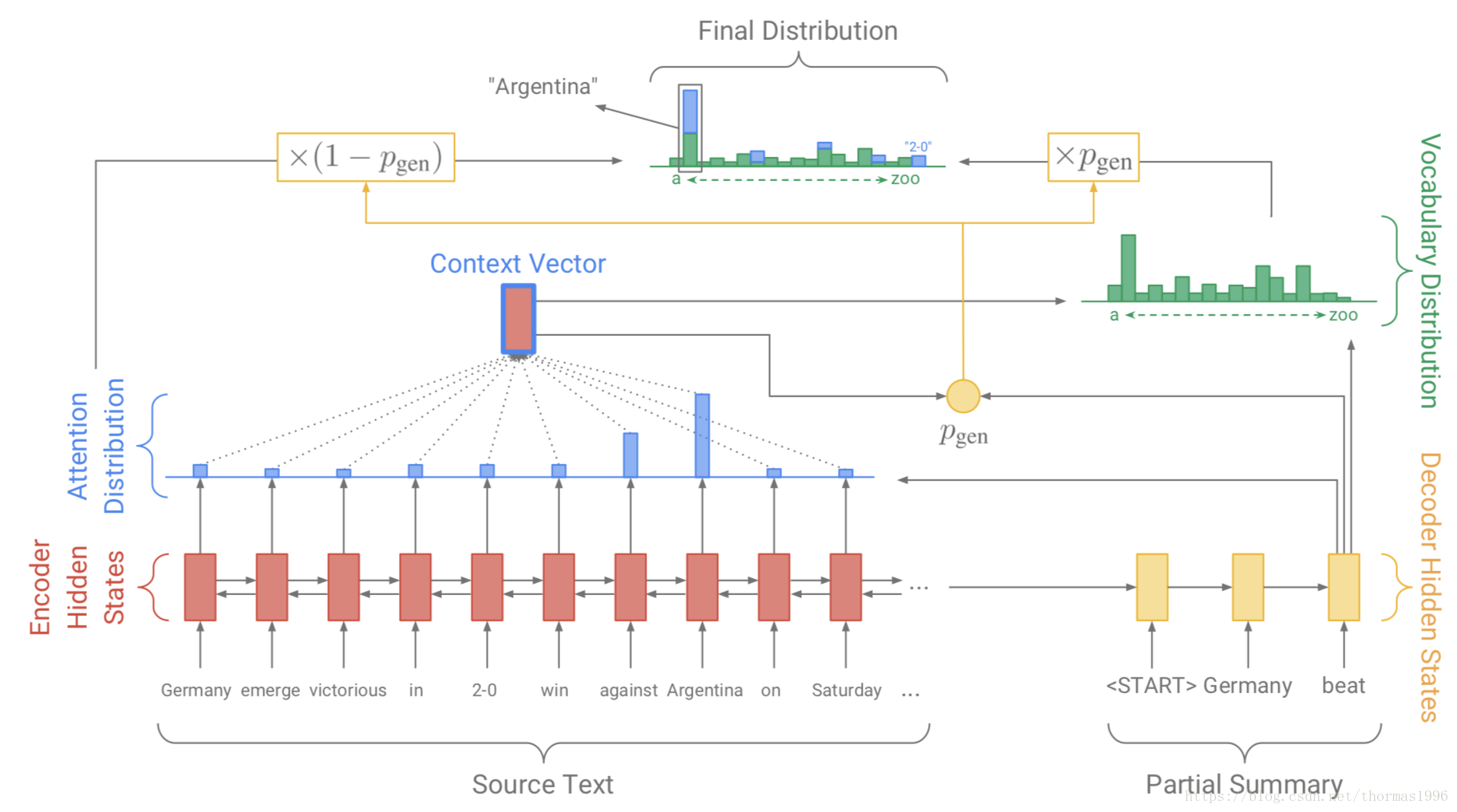
其中$p_{gen}$是pointer softmax，改动的是attention部分：

$e_i^t = v^T tanh(W_hh_i+W_ss_t + w_cc_i^t + b)$

这里的c不是语义向量，是新定义的一个参数：

$c^t = \sum_{t^{'}=1}^{t-1}a^{t^{'}}$

是一个长度为输入长度的向量，第一项是之前时刻输入第一个词attention权重的叠加和，以此类推。加这个参数目的是为了给attention之前生成词的信息，如果之前生成过这些词，那么后续要抑制，通过loss函数加惩罚项实现：
$loss = -logP(w_t*) + \lambda \sum_i \min(a^t,c_i^t)$
原理是如果该词之前出现过了，那么它的$c_i^t$就很大，那么为了减小loss，就需要$a_i^t$变小（因为loss中一项是取两者最小值），$a_i^t$小就意味着这个位置被注意的概率减少。